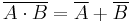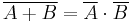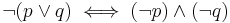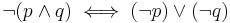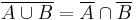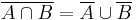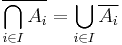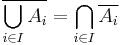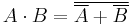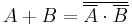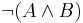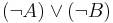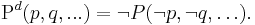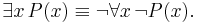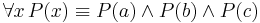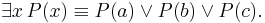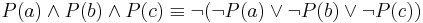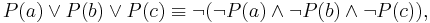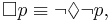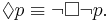De Morgan's laws
In formal logic, De Morgan's laws are rules relating the logical operators "AND" and "OR" in terms of each other via negation. With two operands A and B:
In another form:
- NOT (A AND B) = (NOT A) OR (NOT B)
- NOT (A OR B) = (NOT A) AND (NOT B)
The rules can be expressed in English as:
"The negation of a conjunction is the disjunction of the negations." and
"The negation of a disjunction is the conjunction of the negations."
Contents |
Formal definition
In propositional calculus form:
where:
- ¬ is the negation operator (NOT)
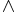 is the conjunction operator (AND)
is the conjunction operator (AND)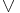 is the disjunction operator (OR)
is the disjunction operator (OR)- ⇔ means logically equivalent (if and only if)
In set theory and Boolean algebra, it is often stated as "Union and intersection interchange under complementation.",[1] which can be formally expressed as:
where:
- A is the negation of A, the overline being written above the terms to be negated
- ∩ is the intersection operator (AND)
- ∪ is the union operator (OR)
The generalized form is:
where I is some, possibly uncountable, indexing set.
In set notation, De Morgan's law can be remembered using the mnemonic "break the line, change the sign".[2]
Substitution form
De Morgan's laws are normally shown in the compact form above, with negation of the output on the left and negation of the inputs on the right. A clearer form for substitution can be stated as:
Or stated as functions:
- P AND Q = NOT( (NOT P) OR (NOT Q) )
- P OR Q = NOT( (NOT P) AND (NOT Q) )
This emphasizes the need to invert both the inputs and the output, as well as change the operator, when doing a substitution.
History
The law is named after Augustus De Morgan (1806–1871)[3] who introduced a formal version of the laws to classical propositional logic. De Morgan's formulation was influenced by algebraization of logic undertaken by George Boole, which later cemented De Morgan's claim to the find. Although a similar observation was made by Aristotle and was known to Greek and Medieval logicians [4] (in the 14th century William of Ockham wrote down the words that would result by reading the laws out[5]), De Morgan is given credit for stating the laws formally and incorporating them in to the language of logic. De Morgan's Laws can be proved easily, and may even seem trivial.[6] Nonetheless, these laws are helpful in making valid inferences in proofs and deductive arguments.
Informal proof
De Morgan's theorem may be applied to the negation of a disjunction or the negation of a conjunction in all or part of a formula.
Negation of a disjunction
In the case of its application to a disjunction, consider the following claim: it is false that either A is true or B is true, which is written as:
In that it has been established that neither A nor B is true, then it must follow that A is not true and B is not true. If either A or B were true, then the disjunction of A and B would be true, making its negation false.
Working in the opposite direction with the same type of problem, consider this claim:
This claim asserts that A is false and B is false (or "not A" and "not B" are true). Knowing this, a disjunction of A and B must be false also. However, the negation of said disjunction yields a true result that is logically equivalent to the original claim. Presented in English, this follows the logic that "Since two things are both false, it is also false that either of them is true."
Negation of a conjunction
The application of De Morgan's theorem to a conjunction is very similar to its application to a disjunction both in form and rationale. Consider the following claim: It is false that A and B are both true, which is written as:
In order for this claim to be true, either or both of A or B must be false, for if they both were true, then the conjunction of A and B would be true, making its negation false. So, the original claim may be translated as "A is false, B is false or both are false", or "'Not A' is true or 'not B' is true, or both".
Presented in English, this would follow the logic that "Since it is false that two things are both true, at least one of them must be false."
Formal proof
By truth table
The laws may be proven directly using truth tables; "1" represents true, "0" represents false.
First we prove: ¬(p ∨ q) ⇔ (¬p) ∧ (¬q).
| p | q | p ∨ q | ¬(p ∨ q) | ¬p | ¬q | (¬p) ∧ (¬q) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Since the values in the 4th and last columns are the same for all rows (which cover all possible truth value assignments to the variables), we can conclude that the two expressions are logically equivalent.
Now we prove ¬(p ∧ q) ⇔ (¬p) ∨ (¬q) by the same method:
| p | q | p ∧ q | ¬(p ∧ q) | ¬p | ¬q | (¬p) ∨ (¬q) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Extensions
In extensions of classical propositional logic, the duality still holds (that is, to any logical operator we can always find its dual), since in the presence of the identities governing negation, one may always introduce an operator that is the De Morgan dual of another. This leads to an important property of logics based on classical logic, namely the existence of negation normal forms: any formula is equivalent to another formula where negations only occur applied to the non-logical atoms of the formula. The existence of negation normal forms drives many applications, for example in digital circuit design, where it is used to manipulate the types of logic gates, and in formal logic, where it is a prerequisite for finding the conjunctive normal form and disjunctive normal form of a formula. Computer programmers use them to simplify or properly negate complicated logical conditions. They are also often useful in computations in elementary probability theory.
Let us define the dual of any propositional operator P(p, q, ...) depending on elementary propositions p, q, ... to be the operator 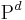 defined by
defined by
This idea can be generalised to quantifiers, so for example the universal quantifier and existential quantifier are duals:
To relate these quantifier dualities to the De Morgan laws, set up a model with some small number of elements in its domain D, such as
- D = {a, b, c}.
Then
and
But, using De Morgan's laws,
and
verifying the quantifier dualities in the model.
Then, the quantifier dualities can be extended further to modal logic, relating the box ("necessarily") and diamond ("possibly") operators:
In its application to the alethic modalities of possibility and necessity, Aristotle observed this case, and in the case of normal modal logic, the relationship of these modal operators to the quantification can be understood by setting up models using Kripke semantics.
See also
- List of Boolean algebra topics
- Isomorphism (NOT operator as isomorphism between positive logic and negative logic)
References
- ^ Boolean Algebra By R. L. Goodstein. ISBN 0486458946
- ^ 2000 Solved Problems in Digital Electronics By S. P. Bali
- ^ DeMorgan’s Theorems at mtsu.edu
- ^ Bocheński's History of Formal Logic
- ^ William of Ockham, Summa Logicae, part II, sections 32 & 33.
- ^ Augustus De Morgan (1806 -1871) by Robert H. Orr